Introduction:

Pendulums are a classic example of simple harmonic motion (SHM), where the restoring force is proportional to the displacement. A coupled pendulum system takes this concept further by introducing interaction between two pendulums. This assignment explores the dynamics of coupled pendulums, deriving the equations of motion and analyzing their behavior.

Theoretical Background:

A coupled pendulum system consists of two simple pendulums of masses m₁ and m₂, suspended from fixed points with lengths l₁ and l₂, respectively. The bobs of the pendulums are connected by a light, rigid spring with a spring constant k.

Diagram:

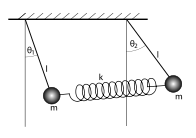
Derivation:

These coupled differential equations govern the motion of the entire system, considering the interaction between the pendulums through the spring.

Analysis:

Analyzing these equations reveals interesting behavior:

• Normal Modes: The coupled system can exhibit normal modes, where both pendulums oscillate at specific frequencies. These normal modes depend on the masses, lengths, and spring constant.
• Energy Transfer: Depending on the initial conditions, energy can oscillate between the two pendulums. One pendulum might be at its maximum displacement while the other is at rest, and then they exchange energy as they swing.

Applications:

The study of coupled pendulums has applications in various fields:

• Vibrational Analysis: Understanding how coupled systems vibrate is crucial in designing bridges, buildings, and other structures that can experience seismic activity or wind loads.
• Molecular Dynamics: Coupled pendulums can be used as a simplified model for studying the vibrational behavior of molecules.
• Synchronization: The concept of normal modes can explain how coupled systems can synchronize their motion under certain conditions.

Conclusion:

The analysis of coupled pendulums demonstrates the complexities that arise when simple systems interact. Understanding these principles is valuable in various scientific and engineering disciplines.